First Token Bias: Transformers as Graphs

The first token bias is not a new problem in Large Language Models (LLMs) literature; however, recent investigations from Google's Deep Mind and University of Oxford suggest why Transformers don’t treat all tokens equally, routing favors at the start of the sequence.

A peculiar and interesting phenomenon that has been spotted across frontier language models is that attention heads often exhibit ‘attention sinks’, where seemingly meaningless tokens – often the first one in the sequence – tend to capture most of the attention. With causal masking, early tokens can broadcast through many layers and positions, while late tokens have only a few short hops to the readout –so their signal gets squeezed (“over-squashing”). As context grows, nearby inputs map to increasingly similar hidden states (representational collapse), erasing distinctions near the tail and hurting tasks where the decisive clue appears last. Viewing the model as a message-passing graph makes this bias explicit: tokens are nodes, attention provides edges, and the topology privileges the head of the prompt. Framed this way, the problem becomes an engineering one,  similar to Graph Neural Networks –improving routes and bandwidth for late tokens  –via architectural tweaks (more global or structured skip connections, position-aware temperature, revised positional geometry, chunk-level processing) and simple prompt tactics (echo key facts early, maintain a running summary) until model-level fixes land.

A simple probe: single-digit copy

What do you think would be the easier task for an LLM?

1. What’s the last digit of 111…10?
   
   
2. What’s the first digit of 011…1?
   
   

(a) ? (b)? Should both be equally easy? Despite that these tasks look trivial for humans, models often wobble –especially as the sequence gets longer. Models tend to get (a) wrong when finding a zero in such a problem because of the representational difference falling toward zero as length increases of 1s –evidence that the model’s internal states become less discriminative over long contexts, making the representations collapse. In other words, the position of this zero actually matters!

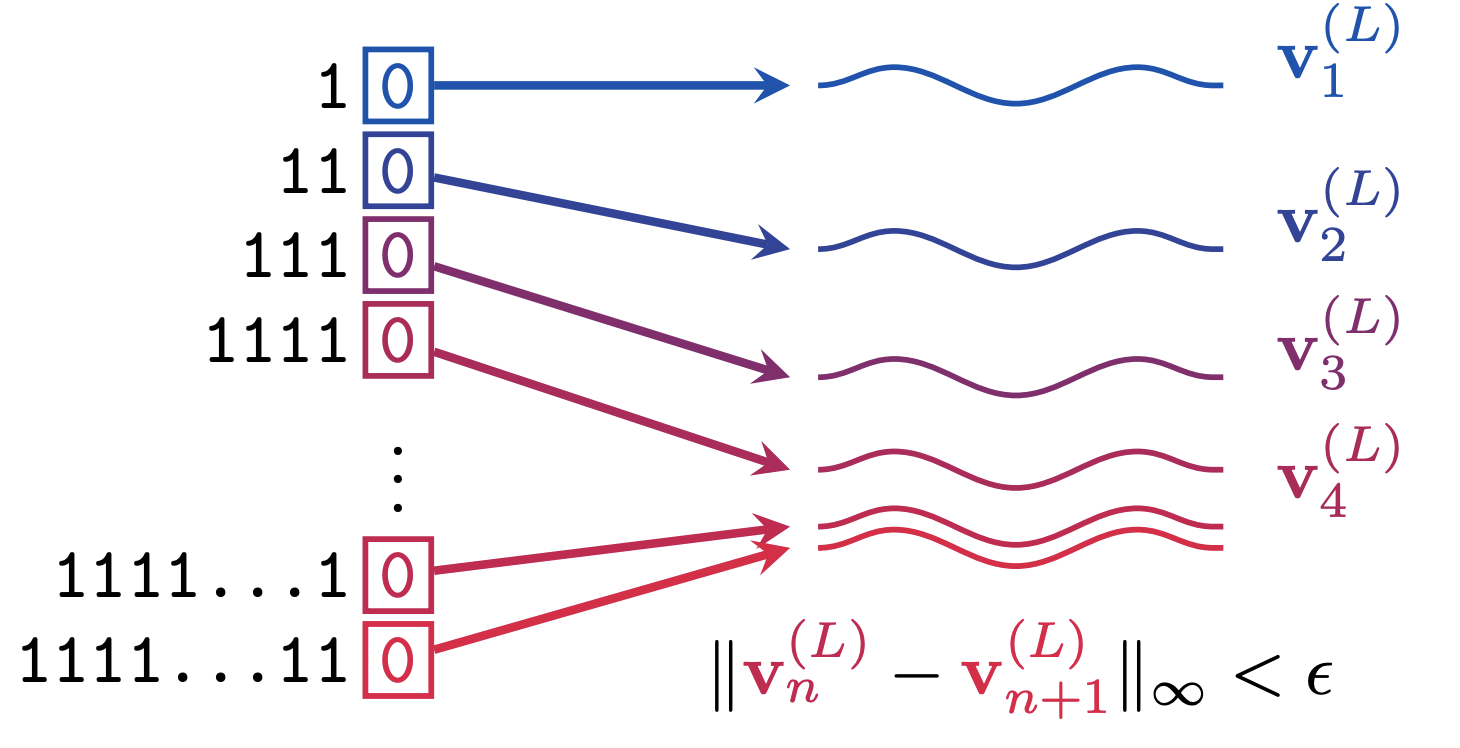
Figure1. Representational collapse with length: For inputs (1,0), the final-layer states (v_n(L), v_n+1(L)) converge –neighboring lengths map to nearly the same vector, given an epsilon there is always an absolute difference of two embeddings less than epsilon – showing how late-token information fades as sequences grow (Image from Barbero et al., 2024).

And as the sequence length increases, the problem gets even worse: representations converge more and more towards the same embedding as shown by Fig. 2.

‍

Figure 2. Counting 1s from a sequence of 1s: As length grows, the mean representational difference rapidly collapses toward the bf16 precision floor, indicating convergence of internal states at long context (shaded band = variability) (Image from Barbero et al., 2024).

‍

Transformers as graphs (and why the first tokens win)

“Over-squashing” was first flagged in graph neural networks: when two nodes are connected by only a few paths, messages get compressed and important detail is lost. A transformer has the same geometry if we view it as a message-passing graph, in a way that we actually think of the transformer as a GNN (Joshi, 2025): each token at each layer is a node, and attention provides the edges in causal masking graph geometry (Fig 6 (left)). At each layer, every token’s state sends a “message” (its value vector) to other tokens, scaled by attention weights on edges defined by the attention pattern. Each receiver aggregates these weighted messages and passes the result to the next layer. Early tokens therefore get many hops to broadcast forward across layers, whereas late tokens have only a few short, congested routes to the readout—setting the stage for over-squashing (See Fig. 3). Later tokens signal is squeezed by information already diffused from earlier tokens, creating a bottleneck. As sequences lengthen, internal states converge toward one another—amplifying bias toward the start of the prompt.

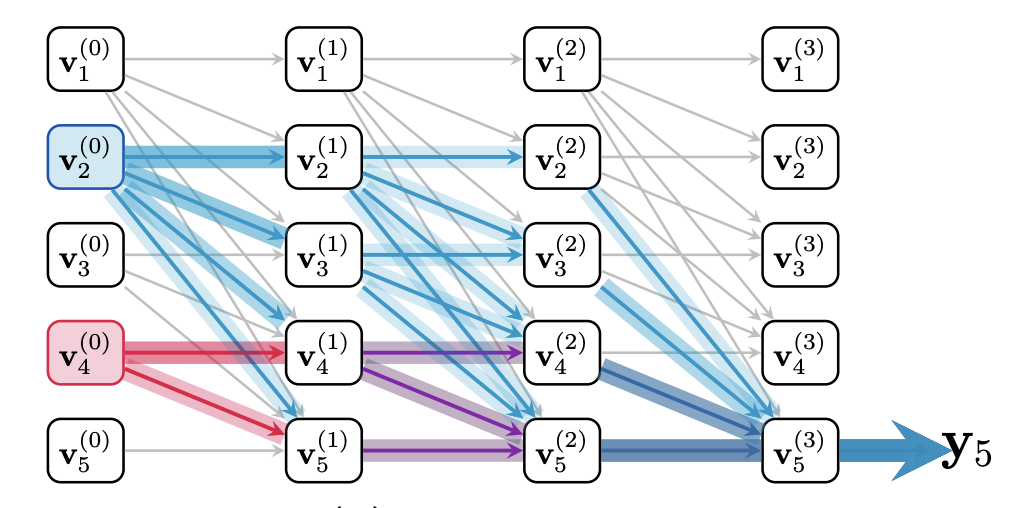
Figure 3. Message-passing view of a causal transformer: each node is a token at a layer. Early tokens (blue) have many multi-layer paths, while later tokens (purple/red) have only a few short, congested routes, illustrating over-squashing and first-token bias (Image from Barbero et al., 2024).

‍

But we have softmax. Doesn’t that fix it?

In standard attention, the mask and pattern (causal, local, global, etc.) define which positions are reachable from a token in one step. The softmax then allocates probability mass over those reachable neighbors. It can sharpen (put most mass on a few) or diffuse (spread mass widely), and in practice it can effectively prune many edges to ~0 weight. But softmax disperse, especially by the number of items in the sequence (Fig. 4) and it can’t create new neighbors or longer paths that the mask/pattern doesn’t already allow. So if late tokens have fewer hops and poorer routes, tuning softmax alone won’t fix that geometry—you need to change the adjacency matrix (i.e., the topology of the graph) (Velickovic et al., 2024). Thus, softmax disperses attention mass but doesn’t guarantee the right topology for long-range propagation. 

‍

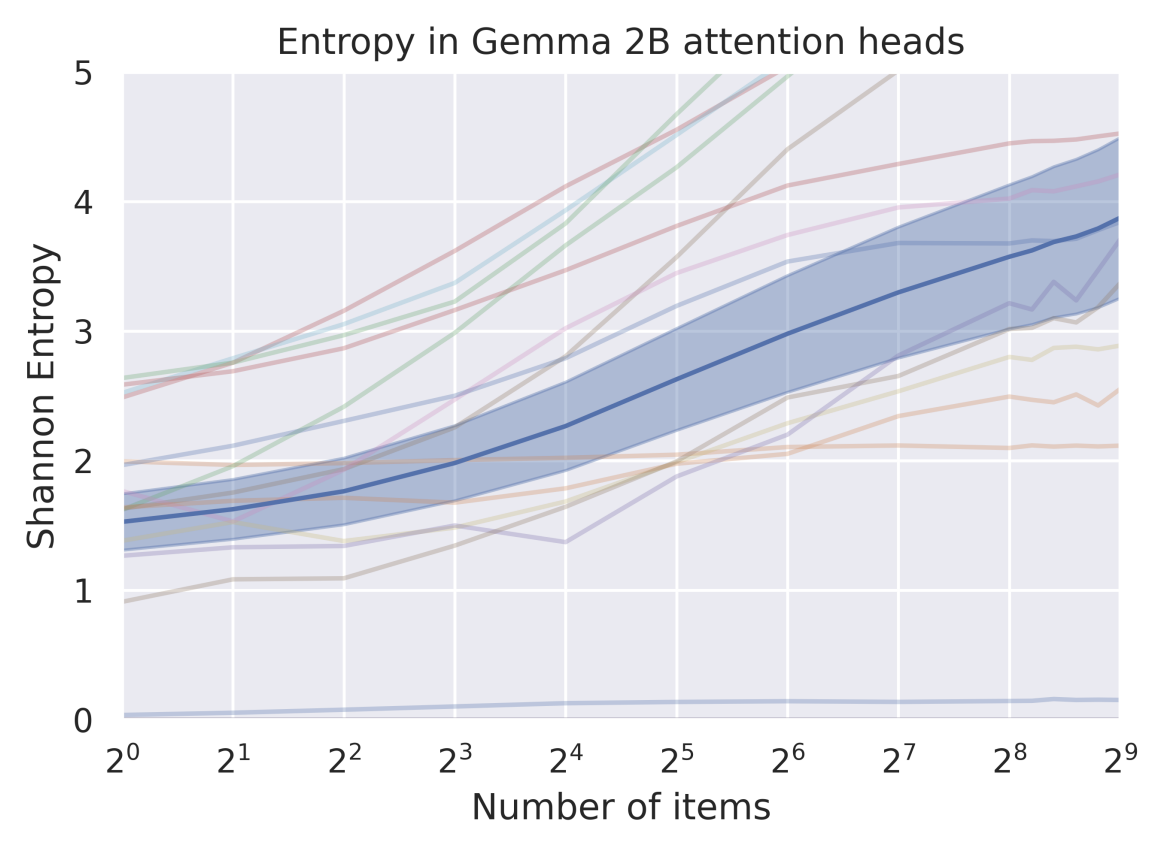
Figure 4. Attention dispersion with length in Gemma-2B, the Shannon entropy of attention heads rises as the number of items grows, showing that attention mass spreads more broadly—becoming diffuse rather than selective—so dispersion alone doesn’t ensure effective long-range routing (Image from Velickovic et al., 2024).

What are the alternatives?

There are several mitigation directions.

1. Global vs. local attention
   The contrasts between global/local patterns across Gemma variants. Predominantly local routing changes the repertoire of possible paths through the model. For late tokens in particular, fewer global connections can mean fewer sinks, decreasing the risk of their signal being squeezed by earlier context. Figure 5, adapted from Ji & Kumar (2025), visualizes this progression in attention wiring across the three variants.

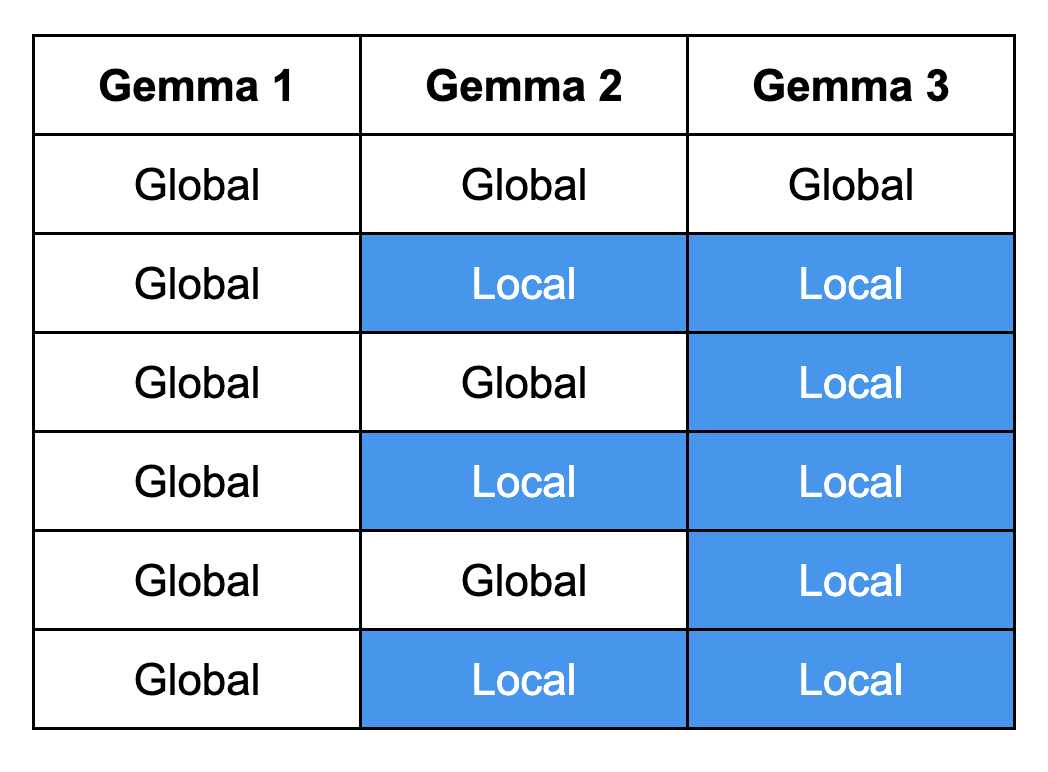
Figure 5. Attention wiring across Gemma variants. Gemma-1 uses all-global layers; Gemma-2 alternates global and local; Gemma-3 starts global then switches mostly to local—showing a shift from dense reach to predominantly local routing (Image from Ji & Kumar 2025).

‍

2. Adaptive temperature across the sequence.

Adjust attention temperature per position or layer so late tokens can sharpen their focus and punch through earlier diffusion. (Veskovie et al., NeurIP 24 SeiForDL).

3. Sparse / structured attention.
   Rather than “spread thin,” allocate few, strong connections that preserve salient routes (e.g., late-to-summary, late-to-early anchors) (Vitvitskyi et al., 2025).
   
   
4. Token-free or chunk-level models.
   If tokens create too many shallow hops, operate on longer units (patches/chunks) or continuous views to shorten effective path length. Fewer steps, stronger messages (Hwang et al., 2025).
   
   
5. Rotary Positional Encoding (RoPE).
   Positional geometry matters—directly shapes the produced graph. Tweaking positional frequency bands can rebalance early/late influence (Barbero et al., ICLR’25). 

Graph rewiring

Rewiring the graph tackles first-token bias by changing who can talk to whom across layers. In causal transformers, early tokens fan out across many hops while late tokens face short, congested routes, so their signal gets squeezed at the readout. Instead of using fully connected causal graphs, we can propose a new way to write tokens connections in transformers: A FunSearch (FS) graph that avoids sinking maintaining context and meaningful semantic connections in a structured, multi-scale wiring with mostly local links plus periodic long-range jumps that create guaranteed highways from the tail to the output. The FunSearch design was discovered using FunSearch algorithm (Romera-Paredes et al., 2023) with some tweaks, the FS graphs preserved mixing but with high fidelity compared to the fully connected graph reducing attention sink (Vitvitskyi et al., 2025). 

Figure 6. Left: Fully connected causal graph: every token attends to all previous tokens, creating dense, global connectivity but at sink cost. Right: FunSearch graph: a structured, multi-scale pattern combining local windows with periodic long-range “jump” connections, preserving efficient global reach while reducing the number of edges and improving routing for late tokens.

‍

References

Barbero, F., Banino, A., Kapturowski, S., Kumaran, D., Araújo, J. G. M., Vitvitskyi, A., Pascanu, R., & Veličković, P. (2024). Transformers need glasses! Information over‑squashing in language tasks (arXiv:2406.04267) [Preprint]. arXiv. https://arxiv.org/abs/2406.04267

Barbero, F., Arroyo, A., Gu, X., Perivolaropoulos, C., Bronstein, M., Veličković, P., & Pascanu, R. (2025). Why do LLMs attend to the first token? (COLM 2025 Conference Paper). arXiv. https://arxiv.org/abs/2504.02732

Barbero, F., Vitvitskyi, A., Perivolaropoulos, C., Pascanu, R., & Veličković, P. (2025). Round and Round We Go! What makes Rotary Positional Encodings useful? (arXiv:2410.06205v2) [Preprint]. arXiv. https://arxiv.org/abs/2410.06205

Hwang, S., Wang, B., & Gu, A. (2025). Dynamic chunking for end-to-end hierarchical sequence modeling (arXiv:2507.07955v2) [Preprint]. arXiv. https://arxiv.org/abs/2507.07955 

Ji, J.-y., & Kumar, R. (2025). Gemma explained: What’s new in Gemma 3. Google Developers Blog. https://developers.googleblog.com/pt-br/gemma-explained-whats-new-in-gemma-3/

Joshi, C. K. (2025). Transformers are Graph Neural Networks (arXiv:2506.22084) [Preprint]. arXiv. https://arxiv.org/abs/2506.22084

Romera-Paredes, B., Barekatain, M., Novikov, A., Li, Z., Banino, A., Elsayed, G. F., … Hassabis, D. (2024). Mathematical discoveries from program search with large language models. Nature, 625(7996), 468–475. https://doi.org/10.1038/s41586-023-06924-6

Veličković, P., Perivolaropoulos, C., Barbero, F., & Pascanu, R. (2025). Softmax is not Enough (for Sharp Size Generalisation) (arXiv:2410.01104v3) [Preprint]. arXiv. https://arxiv.org/abs/2410.01104

Vitvitskyi, A., Araújo, J. G. M., Lackenby, M., & Veličković, P. (2025). What makes a good feedforward computational graph? (arXiv:2502.06751v2) [Preprint]. arXiv. https://arxiv.org/abs/2502.06751